
引言
处理器芯片的本质是数字电路
- 数字芯片 = 处理数字信号的芯片 =
处理
0和1的芯片
需要先理解信息在数字电路中是如何表示, 处理和存储的
- 表示: 数字信号
0和1的含义 - 处理: 门电路和组合逻辑电路
- 存储: 时序逻辑电路
整数的机器级表示
无符号数和有符号数
\[1110_{B}=2^3\times1+2^2\times1+2^1\times1+2^0\times0=14\]
每一个二进制位都代表真值的大小,
这种表示称为无符号二进制整数(unsigned binary integer),
简称无符号数
- 在一个\(n\)位的无符号数中, 最小数是\(0\), 最大数是\(2^n - 1\)
- 之前介绍的加法器, 其实是个无符号数加法器
计算机如何表示负数?
- 数学上是在一个负号
-后添加这个负数的绝对值(如-5) - 计算机只能处理二进制:
- 通过1位来编码整数的符号位, 剩下位用于编码整数的绝对值
- 这种表示称为
有符号二进制整数(signed binary integer), 简称有符号数
原码(sign-and-magnitude)
最高位表示符号位(0为正数, 1为负数),
其余位表示对应真值的绝对值
0b00000111 = 7
0b10000111 = -7
0b00100010 = 34
0b10100010 = -34
# 考虑采用8位的RCA进行原码加法:
0b00000111 (7) 0b10000111 (-7) 0b10000111 (-7) 0b00000111 (7)
+0b00100010 (34) +0b10100010 (-34) +0b00100010 (34) +0b10000111 (-7)
----------- ----------- ----------- -----------
0b00101001 (41) 0b00101001 (41) 0b10101001 (-41) 0b10001110 (-14)观察后得出结论:
- 当两数皆为正数时, RCA所得结果与数学意义一致
- 当两数为负时, RCA所得结果与数学意义不符, 区别在于符号位
- 当仅有一数为负时, RCA所得结果与数学意义不符, 不仅符号位有可能错误, 绝对值也错误
要实现原码加法器, 需要先实现减法器, 并根据两数符号和绝对值的情况, 选择出正确的处理结果
反码(one’s complement)
反码尝试解决原码加法中涉及负数的问题
- 对于正数和
0, 其表示与原码一致 - 对于负数, 其表示为相应相反数的原码的按位取反
0b00000111 = 7
0b11111000 = -7
0b00100010 = 34
0b11011101 = -34
# 考虑采用8位的RCA进行反码加法:
0b00000111 (7) 0b11111000 (-7) 0b11111000 (-7) 0b00000111 (7)
+0b00100010 (34) +0b11011101 (-34) +0b00100010 (34) +0b11111000 (-7)
----------- ----------- ----------- -----------
0b00101001 (41) 0b11010101 (-42) 0b00011010 (26) 0b11111111 (-0)观察后得出结论:
- 当两数皆为正数时, RCA所得结果与数学意义一致
- 当有一数为负时, RCA所得结果与数学意义不符, 虽然符号位正确, 但绝对值部分不正确
反码加法器
0b00000111 (7) 0b11111000 (-7) 0b11111000 (-7) 0b00000111 (7)
+0b00100010 (34) +0b11011101 (-34) +0b00100010 (34) +0b11111000 (-7)
----------- ----------- ----------- -----------
0b00101001 (41) 0b11010101 (-42) 0b00011010 (26) 0b11111111 (-0)- 特别地, 当互为相反数的两数相加时, 结果总是
0b11111111- 按反码解释, 所得结果的真值为
-0 - 如果将其看成数学意义上的
0, 则RCA结果正确
- 按反码解释, 所得结果的真值为
让-0作为RCA的输入进行计算, 又会得到不正确的结果:
反码加法器的一种实现方式:
- 将反码转换为真值等价的原码
- 使用原码加法器计算结果
- 将结果转换为真值等价的反码
补码(two’s complement)
补码进一步修复了反码计算错误时结果的偏差
- 对于正数和
0, 其表示与原码一致 - 对于负数, 其表示为相应相反数的原码的按位取反后加
1
- 对于\(n\)位的补码,
最大数是
0b011...11, 对应的真值是\(2^{n-1}-1\) - 最小数是
0b100...00, 对应的真值是\(-2^{n-1}\)- 在补码中, 最小数很特殊,
不能通过对某个正数进行
取反加1来得到 - 以8位补码为例, 最大数
0b01111111=127- 对其进行
取反加1, 得到的是0b10000001=-127
- 对其进行
- 而最小数
0b10000000=-128, 对其进行取反加1, 得到的是0b01111111+1=0b10000000=-128, 与其自身相同
- 在补码中, 最小数很特殊,
不能通过对某个正数进行
补码的加权求和展开式
设某正数\(p\)的补码表示为\(\mathrm{0b}0p_{n-2}p_{n-3}\dots p_1p_0\), 并设其相反数\(q\)的补码表示为\(\mathrm{0b}1q_{n-2}q_{n-3}\dots q_1q_0\)
根据补码的定义, 有 \[\mathrm{0b}q_{n-2}q_{n-3}\dots q_1q_0=\mathrm{0b}\overline{p_{n-2}}\overline{p_{n-3}}\dots\overline{p_1}\overline{p_0}+1\] 其中\(\overline{p_i}\)表示\(p_i\)的按位取反
将两侧的二进制表示加权展开, 有 \[\sum_{i=0}^{n-2}2^iq_i=\sum_{i=0}^{n-2}2^i\overline{p_i}+1\]
补码的加权求和展开式(2)
此外, 由于\(p_i\)为0或1,
故\(\overline{p_i}\)为1或0,
因此有\(p_i+\overline{p_i}=1\)
考虑\(q\)的真值, 有 \[\begin{array}{ll} q&\displaystyle=-p=-(\mathrm{0b}0p_{n-2}p_{n-3}\dots p_1p_0)=-\sum_{i=0}^{n-2}2^ip_i \\ &\displaystyle=-\sum_{i=0}^{n-2}2^i(1-\overline{p_i})=-\sum_{i=0}^{n-2}2^i+\sum_{i=0}^{n-2}2^i\overline{p_i} \\ &\displaystyle=-(2^{n-1}-1)+\sum_{i=0}^{n-2}2^i\overline{p_i}=-2^{n-1}+(\sum_{i=0}^{n-2}2^i\overline{p_i}+1) \\ &\displaystyle=-2^{n-1}+\sum_{i=0}^{n-2}2^iq_i \\ \end{array}\]
补码的加权求和展开式(3)
\[q=\mathrm{0b}1q_{n-2}q_{n-3}\dots q_1q_0=-2^{n-1}+\sum_{i=0}^{n-2}2^iq_i\]
结论: 补码的符号位可以以\(-2^{n-1}\)为权来展开, 从而求得补码的真值
例如, 用这种方式对0b11111001加权展开, 则有 \[-2^7+2^6+2^5+2^4+2^3+2^0=-7\]
与编码的真值一致
补码加法器
# 考虑采用8位的RCA进行补码加法
0b00000111 (7) 0b11111001 (-7) 0b11111001 (-7) 0b00000111 (7)
+0b00100010 (34) +0b11011110 (-34) +0b00100010 (34) +0b11111001 (-7)
----------- ----------- ----------- -----------
0b00101001 (41) 0b11010111 (-41) 0b00011011 (27) 0b00000000 (0)观察后得出结论: 用RCA计算补码加法时, 即使输入包含负数, RCA所得结果仍然符合数学意义
进一步地: 可以用RCA来计算补码的减法!
- 在数学意义上, 有
A-B=A+(-B) - 上文说明了, 无论
A和B为何值, RCA所得结果都符合数学意义 - 故: 用RCA计算
A+(-B)= 数学意义上的A+(-B)= 数学意义上的A-B
正是由于可以用同一个加法器电路来计算补码的加法和减法, 现代计算机中普遍用补码来表示整数
为什么补码可以?
以4位二进制数为例, 将二进制数按顺时针顺序排列(时钟模型):
0000 (0)
(-1) 1111 0001 (1)
(-2) 1110 ^ 0010 (2)
(-3) 1101 | 0011 (3)
(-4) 1100 + 0100 (4)
(-5) 1011 0101 (5)
(-6) 1010 0110 (6)
(-7) 1001 0111 (7)
1000 (-8)RCA是在二进制层次上进行加法:
- 加一个正数\(n\), 相当于把指针按顺时针方向拨动\(n\)格
- 加一个负数\(-n\), 相当于把指针按逆时针方向拨动\(n\)格
要让某种编码的加法结果符合数学意义, 就要让其真值也按顺时针递增
上图的括号()展示了补码的例子:
- 只要不跨越
7和-8之间的边界, 用RCA计算的结果总是符合数学意义
为什么原码和反码不行?
原码 反码
0000 (0) 0000 (0)
(-7) 1111 0001 (1) (-0) 1111 0001 (1)
(-6) 1110 ^ 0010 (2) (-1) 1110 ^ 0010 (2)
(-5) 1101 | 0011 (3) (-2) 1101 | 0011 (3)
(-4) 1100 + 0100 (4) (-3) 1100 + 0100 (4)
(-3) 1011 0101 (5) (-4) 1011 0101 (5)
(-2) 1010 0110 (6) (-5) 1010 0110 (6)
(-1) 1001 0111 (7) (-6) 1001 0111 (7)
1000 (-0) 1000 (-7)原码存在两个问题:
- 真值在
0b0000和0b1111之间不连续 => 计算0+(-1), 得到-7 - 负数的编码方式让真值按顺时针递减 => 计算
(-4)+1, 得到-5
反码通过取反操作修复了问题2, 但问题1仍然存在
- 真值在
0b0000和0b1111之间不连续 => 计算0+(-1), 得到-0
补码通过编码上的+1操作, 将负数真值往顺时针转动1格,
修复了问题1
补码加法的溢出
即使是补码, 也存在编码连续但真值不连续的边界
- 即最大数
0b0111...111和最小数0b1000...000之间的边界
如果加法的计算跨越了这个边界, 所得结果将与数学意义不符
这个边界是必然存在的:
- 对于给定的二进制位数, 其表示范围总是有限的
- 必定存在超过表示范围的数值, 使得真值的分布无法一直连续
这种计算结果超过编码表示范围的情况,
称为溢出(overflow)
- 为了检查加法计算的结果是否符合数学意义, 电路需要检测是否发生溢出
溢出检测
从时钟模型的角度来看, 跨越不连续边界分两种情况:
- 在正数部分往顺时针方向拨动指针, 跨越到负数部分
- 在负数部分往逆时针方向拨动指针, 跨越到正数部分
从数学意义的角度来看, 这两种情况分别对应:
- 两个正数相加, 结果为负数
- 两个负数相加, 结果为正数
在真值表中考虑符号位的加法情况, 即可检查是否发生溢出!
| \(A_{n-1}\) | \(B_{n-1}\) | \(C_{n-1}\) | \(|\) | \(C_n\) | \(S_{n-1}\) | 溢出 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | \(|\) | 0 | 0 | 否 |
| 0 | 0 | 1 | \(|\) | 0 | 1 | 是 |
| … | … | … | \(|\) | … | … | … |
时序逻辑电路
组合逻辑 vs. 时序逻辑
- 组合逻辑电路的输出完全由当前输入决定
- 可实现各种运算功能
- 新需求: 如何实现电子表中
新的秒数 = 旧的秒数 + 1?
我们需要新的电路特性:
- 可以读出电路的旧状态
- 可以更新电路的状态
- 组合逻辑电路没有新旧状态的概念
- 需要通过时序逻辑电路实现 - 可以存储状态的电路
交叉配对反相器(Cross-Coupled Inverters)
\(Q\)和\(\overline{Q}\)分别经过两个反相器后, 保持不变
- 可稳定地存储1 bit信息(通过\(Q\)端输出)

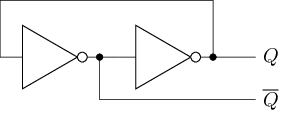
- \(Q=0, \overline{Q}=1\),
则认为存储
0; \(Q=1, \overline{Q}=0\), 则认为存储1
如果从某时刻开始, \(Q=\overline{Q}=0\), 会怎样?
- 经过一定延迟后, \(Q=\sim \overline{Q}_{prev}=1\), \(\overline{Q}=\sim Q_{prev}=1\)
- 再经过一定延迟后, \(Q=\sim \overline{Q}_{prev}=0\), \(\overline{Q}=\sim Q_{prev}=0\)
- 电路处于震荡状态, 无法表示稳定的信息(也称亚稳态)
- 也有可能因物理制造方面的不对称因素(如线延迟, 晶体管尺寸等), 导致电路收敛到其中一个稳定状态, 但收敛时间难以预测
不过, 即使上述电路位于稳定状态, 也使无法更新\(Q\)和\(\overline{Q}\)
更实用的存储单元 - SR锁存器
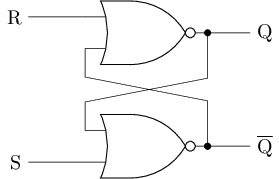
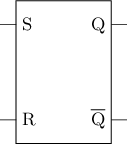
| S | R | \(|\) | Q |
|---|---|---|---|
| 0 | 0 | \(|\) | 保持 |
| 0 | 1 | \(|\) | 0 |
| 1 | 0 | \(|\) | 1 |
| 1 | 1 | \(|\) | 禁止 |
S(et)R(eset)锁存器, 其中S和R用于控制锁存器的状态
#T(SR latch) = 2#T(nor) = 2 * 6 = 12不允许S=R=1
- 或非门的特性使输出均为0
- 从S=R=1变为S=R=0时, 会进入亚稳态
- 真实电路可能会受随机扰动而进入某个稳定状态, 但无法提前预知
- 此时电路的行为是未定义的, 每次工作可能会产生不同的结果
避免亚稳态 - D锁存器
思想: 额外添加两个与门, 将SR锁存器的4种输入限制成3种合法输入
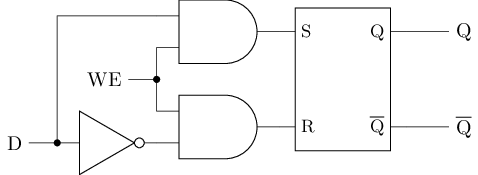
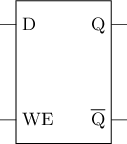
- D为输入数据
- WE为写使能(Write Enable)
- 写使能有效时, 将D的当前值写入锁存器
- 写使能无效时, 锁存器保持不变
| WE | D | \(|\) | S | R | \(|\) | Q |
|---|---|---|---|---|---|---|
| 0 | 0 | \(|\) | 0 | 0 | \(|\) | 保持 |
| 0 | 1 | \(|\) | 0 | 0 | \(|\) | 保持 |
| 1 | 0 | \(|\) | 0 | 1 | \(|\) | 0 |
| 1 | 1 | \(|\) | 1 | 0 | \(|\) | 1 |
#T(D latch) = #T(SR latch) + 2#T(and) + #T(not) = 12 + 2 * 8 + 2 = 30用与非门搭建的D锁存器
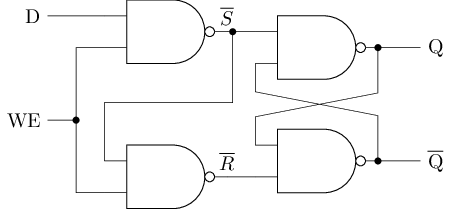
#T(D latch) = 4#T(nand) = 4 * 6 = 24面积更小
| WE | D | \(|\) | \(\overline{S}\) | \(\overline{R}\) | \(|\) | Q |
|---|---|---|---|---|---|---|
| 0 | 0 | \(|\) | 1 | 1 | \(|\) | 保持 |
| 0 | 1 | \(|\) | 1 | 1 | \(|\) | 保持 |
| 1 | 0 | \(|\) | 1 | 0 | \(|\) | 0 |
| 1 | 1 | \(|\) | 0 | 1 | \(|\) | 1 |
用传输门搭建的D锁存器
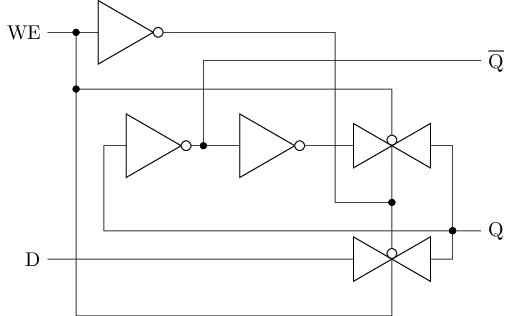
WE=1时, 下方传输门导通, 上方传输门截止,Q=DWE=0时- 上方传输门导通, 形成交叉配对反相器, 锁存当前
Q的值 - 下方传输门截止, 输入
D无法影响锁存的值
- 上方传输门导通, 形成交叉配对反相器, 锁存当前
#T(D latch) = 3#T(not) + 2#T(tg) = 3 * 2 + 2 * 2 = 10复杂系统中的同步关系
一个复杂系统包含多个模块, 需要考虑如何控制多个模块协同工作
- 例如, 某系统包含3个模块: 读数据模块, 加法模块和写结果模块
- 我们期望按顺序发生以下事件
- 读数据模块先工作
- 读出数据后, 加法模块才开始计算
- 加法模块的结果计算好后, 再将结果写入目标存储元件
需要正确实现一种同步关系
- 事件A在事件B之后发生(happened after)
需要额外的机制来实现同步关系
同步电路 = 通过全局的时钟信号实现同步关系
时钟信号 = 在高低电平之间来回翻转的脉冲信号
- 一次高电平和一次低电平合起来称为一个周期
- 从低电平翻转为高电平, 称为正边沿(positive edge)或上升沿
- 从高电平翻转为低电平, 称为负边沿(negative edge)或下降沿
+--- positive edge +--- negative edge
V V
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| | | | | | | | | | | | | | | |
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +同步电路: 通过全局时钟信号实现同步关系
- 存储单元仅在时钟边沿到达时写入数据
- 且能在后续时钟周期中稳定读出该数据
时钟信号的不同周期存在天然的先后顺序
- 同步电路的设计 = 把需要同步的事件划分到不同的周期中, 由时钟信号来控制这些事件的先后顺序
同步电路 vs. 异步电路
异步电路 = 通过模块之间的局部通信信号实现同步关系
在同步电路中, 所有模块都在时钟信号的控制下工作
- 容易实现同步关系, 因此设计简单
- 由于存在时钟信号, 电路分析方法也容易(如分析工作频率等)
- 但时钟信号时周期性翻转的, 引入较高的功耗
和同步电路相比, 异步电路:
- 无时钟开销, 功耗低
- 但设计和分析较困难
同步电路被业界广泛采用
仅靠D锁存器无法实现同步电路的特性
同步电路: 存储单元仅在时钟边沿到达时写入数据, 且在该时钟周期中稳定读出该数据
D锁存器的性质: WE有效时, 输入的变化马上传播到输出
将时钟连到D锁存器的WE端仍然无法实现
- 假设上升沿触发
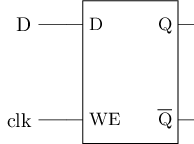
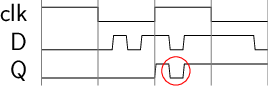
锁存器属于电平触发(level-triggered)的存储元件
- 只要输入发生变化, 锁存器就能立即感知, 并将该变化传播到输出端
我们需要一种边沿触发(edge-triggered)的存储元件
- 只有信号边沿到来时, 才将输入传播到输出端
D触发器(D Flip-Flop, DFF)
- 一种边沿触发的存储元件,
可以在时钟信号维持电平的时刻巧妙地阻塞输入信号的传播
- 逻辑符号左下方的
>表示该端口需要连接时钟信号
- 逻辑符号左下方的
- D触发器有多种实现方式, 这里介绍主从式D触发器
- 由两个D锁存器构成, 左边为主锁存器, 右边为从锁存器
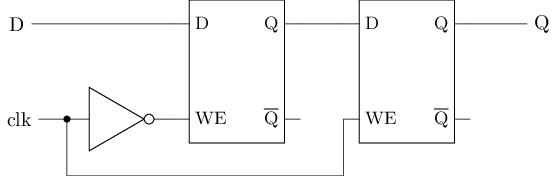
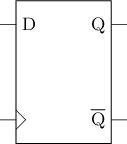
#T(DFF) = 2#T(D-latch) + #T(not) = 2 * 10 + 2 = 22D触发器的工作过程

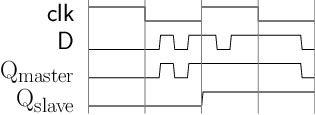
- 数据准备阶段
clk为低电平, 主锁存器WE有效,D可从外部进入主锁存器- 由于从锁存器
WE无效, 故D无法传播到从锁存器 - 整个D触发器的输出端
Q保持不变
D触发器的工作过程(2)


- 采样阶段
- 当
clk上升沿到来, 主锁存器WE无效,D无法从外部进入主锁存器D的后续变化将无法对主锁存器造成影响- 从而将时钟信号上升沿到来前的外部数据
D“锁”在主锁存器中
- 从锁存器
WE开始有效, 主锁存器中 “锁住”的数据将传播到从锁存器- 并作为整个D触发器的输出
- 当
D触发器的工作过程(3)


- 维持阶段
clk为高电平, 主锁存器WE无效, 不受D变化的影响- 从锁存器
WE虽然有效, 但由于输入保持不变, 故输出也保持不变 - 整个D触发器的输出端
Q保持不变
D触发器符合同步电路对存储元件的要求
- 是同步电路设计中的基本存储元件
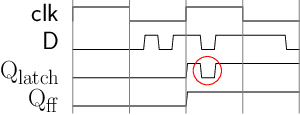
带复位端的D触发器
复位端有效时, 可将D触发器清零
其中, resetn为低电平有效的复位信号
- 当
resetn为1时, 其功能与之前的D触发器相同 - 当
resetn为0时, 将往D触发器写入0
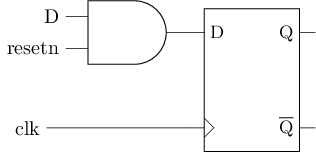
#T(DFFR) = #T(DFF) + #T(and) = 22 + 8 = 30
即使resetn为0,
也需要等待clk上升沿到来时, 才会清零
- 如果
resetn信号在clk上升沿到来前就撤销, 将不会发生清零
这种复位方式称为同步复位
- 复位信号需要与时钟保持同步, 复位功能才生效
- 相应地, 有
异步复位方式
异步复位方式的D触发器
在复位信号有效时, 马上将D触发器清零, 不必等待时钟上升沿到来
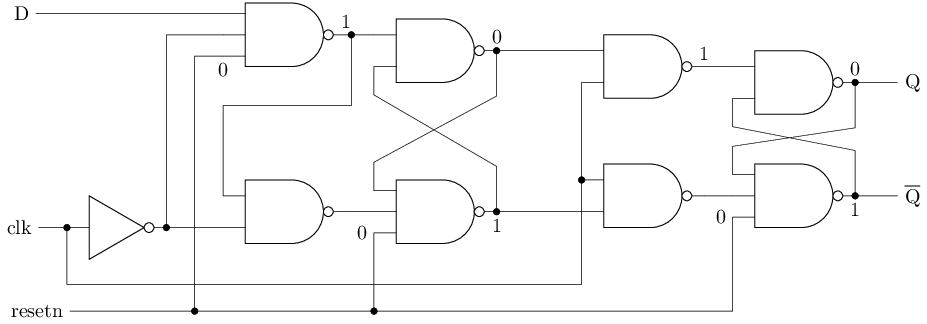
带置位端的D触发器
置位端有效时, 可将D触发器置1
- 类似地, 分
同步置位和异步置位两种方式
异步置位信号setn有效时,
主锁存器和从锁存器中存储的值直接变为1
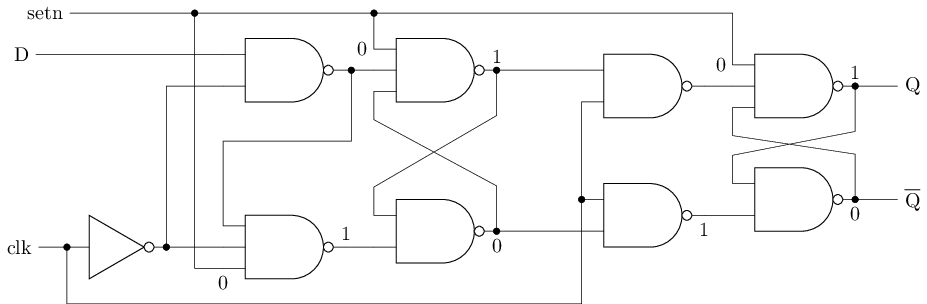
两种复位/置位方式对电路的时序有不同影响, 暂不深入讨论
带使能端的D触发器
EN有效时, 选择外部数据D作为D触发器的输入EN无效时, 选择D触发器中存储的当前数据作为D触发器的输入- 也即, D触发器中存储的值保持不变
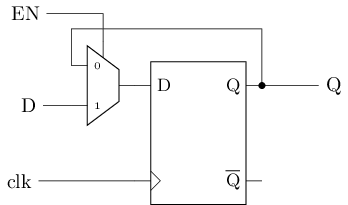
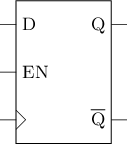
#T(DFFE) = #T(DFF) + #T(2-1 mux) = 22 + 6 = 28寄存器 = 可同时读写多位的结构
由多个D触发器组成
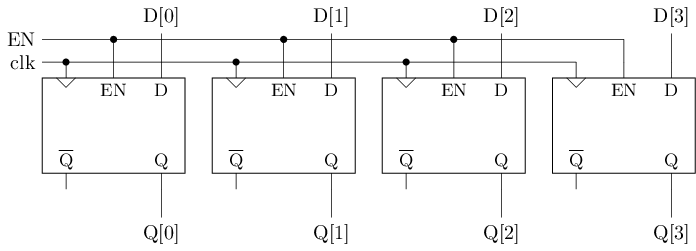
可采用带复位端或置位端的D触发器, 实现寄存器的初始化
- 如
9=0b1001, 可依次采用DFFS, DFFR, DFFR, DFFS来构成4位寄存器, 使其在电路复位后存储9
一个32位无初值的寄存器所需的晶体管数量约为:
#T(reg32) = 32#T(DFFE) = 32 * 28 = 896关于面积的说明
除了对等设计原则, 实际的电路(如标准单元库)仍然需要考虑其他电气特性
- 因此需要添加更多的反相器作为驱动单元
#T(x)的计算并未考虑这些反相器
- 因此和实际情况相比,
#T(x)对面积的估计是偏低的 - 追求更精确的
#T(x)需要考虑过多细节- 因此
#T(x)仅用于进行大致的估算
- 因此
在真实的项目中, 通常由EDA工具读取标准单元库的面积数据来进行面积评估
- 用户无需自行计算晶体管的面积和数量
总结
总结
- 整数的机器级表示
- 原码 - 最高位表示符号位, 其余位表示对应真值的绝对值
- 反码 - 正数和
0与原码一致, 负数为相应相反数的原码的按位取反 - 补码 - 正数和
0与原码一致, 负数为相应反码加1 - 用时钟模型分析不同编码的问题
- 补码加法的溢出检测
- 时序逻辑电路
- 交叉配对反相器能存储信息, 但不能更新
- SR锁存器能更新信息, 但输入不当时存在亚稳态的风险
- D锁存器可以避免输入导致的亚稳态, 但不满足同步电路的要求
- D触发器符合同步电路的要求, 是同步电路设计中的基本存储元件
- 带(同步/异步)复位/置位端的D触发器, 带使能端的D触发器


