引言
处理器芯片的本质是数字电路
- 数字芯片 = 处理数字信号的芯片 =
处理
0和1的芯片
需要先理解信息在数字电路中是如何表示, 处理和存储的
- 表示: 数字信号
0和1的含义 - 处理: 门电路和组合逻辑电路
- 存储: 时序逻辑电路
通过晶体管实现0和1
数字电路由晶体管构成
0和1是两个抽象的概念
- 在数字电路中,
0和1的表示和晶体管有关
金属-氧化物-半导体场效应晶体管(Metal-Oxide-Semiconductor Field-Effect Transistor, MOSFET)
- 分nMOS(下图, 为侧视图)和pMOS两种
- 都有栅极, 源极, 漏极
晶体管\(\approx\)生活中的开关
- 栅极的电压\(\approx\)手
- 源极和漏极\(\approx\)开关连接的两端
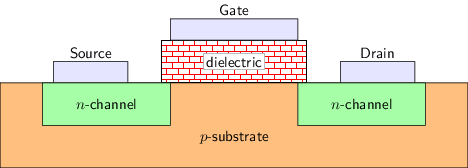
- 通过控制栅极的电压, 来控制源极和漏极是否连通
用高中知识理解晶体管的开关原理
- 以nMOS为例, 在源极和漏极中添加磷元素, 磷元素容易失去一个电子后与硅形成共价键
- 给栅极加电压时, 在绝缘体下方形成电场, 吸引电子聚集在绝缘体下方
- 聚集的电子足够多, 形成沟道, 连通源极和漏极

- 根据电气特性, nMOS的功能为
- 当\(V_G-V_S\)较大时, 源极和漏极导通 - 开关合上
- 当\(V_G-V_S\)较小时, 源极和漏极截止 - 开关断开

- pMOS的功能表现类似: \(V_S-V_G\)较大时导通, \(V_S-V_G\)较小时截止
CMOS = 用MOS管的开关特性实现0和1
CMOS = Complementary MOS = nMOS + pMOS
最简单的CMOS电路:

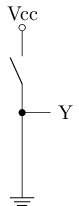
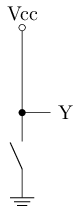
- A点加高电压时, n管导通, p管截止, 相当于Y点与地相连, 电压低
- A点加低电压时, n管截止, p管导通, 相当于Y点与电源相连, 电压高
CMOS将nMOS和pMOS的开关特性转换成输出电压的高低
- 将物理上的高电压定义为逻辑
1(高电平), 低电压定义为逻辑0(低电平)
我们得到了数字电路中信号的两种基本状态!
通过晶体管搭建门电路
门电路 = 对状态进行运算
光有0和1还不够, 还要进行运算
- 通过CMOS电路对
0和1进行各种有意义的转换
- 考虑之前的CMOS电路:
- A点为
1时, n管导通, p管截止, Y点为0 - A点为
0时, n管截止, p管导通, Y点为1
- A点为

这正好是逻辑上的非运算!
- 这个电路就是非门, 也称反相器

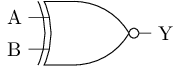
另一个门电路
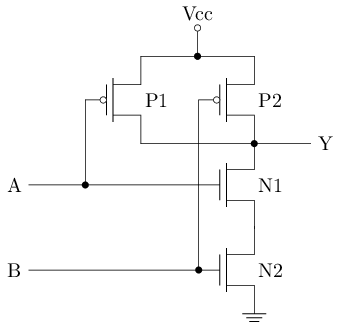
- P1和P2并联, 其中一者导通时, Y为
1 - N1和N2串联, 两者均导通时, Y为
0
| A | B | P1 | P2 | N1 | N2 | Y |
|---|---|---|---|---|---|---|
| 0 | 0 | 导通 | 导通 | 截止 | 截止 | 1 |
| 0 | 1 | 导通 | 截止 | 截止 | 导通 | 1 |
| 1 | 0 | 截止 | 导通 | 导通 | 截止 | 1 |
| 1 | 1 | 截止 | 截止 | 导通 | 导通 | 0 |
这正好是逻辑上的与非运算!
- 这个电路就是与非门

与门 = 与非门 + 非门


| A | B | P1 | P2 | N1 | N2 | Y0 | P3 | N3 | Y |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 导通 | 导通 | 截止 | 截止 | 1 | 截止 | 导通 | 0 |
| 0 | 1 | 导通 | 截止 | 截止 | 导通 | 1 | 截止 | 导通 | 0 |
| 1 | 0 | 截止 | 导通 | 导通 | 截止 | 1 | 截止 | 导通 | 0 |
| 1 | 1 | 截止 | 截止 | 导通 | 导通 | 0 | 导通 | 截止 | 1 |
或非门和或门

- P1和P2串联, 两者均导通时, Y为
1 - N1和N2并联, 其中一者导通时, Y为
0
| A | B | P1 | P2 | N1 | N2 | Y |
|---|---|---|---|---|---|---|
| 0 | 0 | 导通 | 导通 | 截止 | 截止 | 1 |
| 0 | 1 | 导通 | 截止 | 截止 | 导通 | 0 |
| 1 | 0 | 截止 | 导通 | 导通 | 截止 | 0 |
| 1 | 1 | 截止 | 截止 | 导通 | 导通 | 0 |
这正好是逻辑上的或非运算!
或非门的输出连一个非门, 可组成或门
传输门
由一对n管和p管并联组成
- 其中C和C\({}^\prime\)为一对互补的控制信号
- C为
1时, P和N均导通, 此时A和B连通 - C为
0时, P和N均截止, 此时A和B断开


异或操作
异或(XOR)操作的两种理解:
异表示不同, 输入不同结果为1, 否则为0- 在
或的基础上, 排除输入均为1的情况- 因此也称
排斥或(eXclusive OR) 或也称相容或, 允许输入均为1
- 因此也称
| A | B | Y | 描述 |
|---|---|---|---|
| 0 | 0 | 0 | ~A & ~B |
| 0 | 1 | 1 | ~A & B |
| 1 | 0 | 1 | A & ~B |
| 1 | 1 | 0 | A & B |
从真值表得到逻辑表达式的步骤:
- 对于真值表中的每个表项, 考虑每个输入, 若为
1, 则取输入信号本身; 若为0, 则取输入信号的非. 对这些信号进行与, 得到该表项的描述 - 考虑真值表中输出为
1的表项, 对这些表项的描述进行或运算即可
异或操作的逻辑表达式为:
Y = A ^ B = (~A & B) | (A & ~B)
异或门
在门电路层面, Y=(~A&B)|(A&~B)
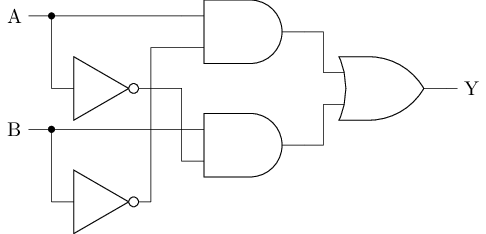
在晶体管层面搭建, 效果更优
A=1时, P2和N2相当于非门; 传输门截止; 故此时Y=~BA=0时, P2和N2均截止; 传输门导通; 故此时Y=B

门电路的面积
CMOS电路的对等设计原则
0和1的电气特性应当一致
- 输出
1所产生的电流, 应当与输出0所吸收的电流一致- 即\(I_{Y=1}=-I_{Y=0}\)
- 输出
1时电流经过p管所产生的电压降, 应当与输出0时电流经过n管所产生的电压降一致- 即\(V_{CC}-V_{Y=1}=V_{Y=0}-V_{GND}\)

若不满足对等设计原则, 不同拓扑位置的同一种门电路,
其电气特性可能不同

- 例如, \(V_A\)可能不满足第3个非门的栅极电压工作条件, 使电路失效
对等设计原则使得CMOS电路的使用者只需关心电路逻辑,
而不必过多关心电气特性
门电路的面积
回顾之前对#T(x)的定义, 有
要满足对等设计原则, 门电路中不同位置的晶体管, 尺寸可能不同
- 定义一个最小晶体管模型, 将其面积定义为
单位1- 为了简化, 此处认为最小p管和最小n管的面积相同(实际上前者稍大)
- 重新定义
#T(x), 记其为门电路x中包含的等效最小晶体管的数量
非门的拓扑结构是对称的, 采用最小晶体管仍符合对等设计原则
- 无论何者导通, 电流只会经过其中一个晶体管, 产生的电压降均相同
- 故仍有
#T(not) = 2

门电路的面积(2)
与非门的拓扑结构并非对称
- 当n管导通时, 电流需要经过两个串联的晶体管
- 若n管尺寸与p管相同, 在电流对等的情况下,
电流经过两个n管所产生的电压降, 是p管导通时的2倍
- 此时电压降不满足对等设计原则

为了满足对等设计原则, 应调整n管, 使得每个n管的电阻是原来的一半
- 例如, 增加n管的尺寸, 或将原来的每个n管分别替换为两个并联的n管
- 也即, 当P1和P2采用最小晶体管时, N1应采用两个最小晶体管进行并联, N2也如此
三输入与非门
在门电路层面搭建
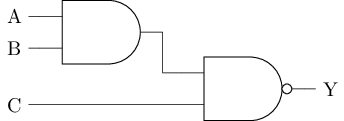
进位计数法
进位计数法
物理世界并非只有0和1,
需要考虑如何用0和1来表示各种信息
- 这些表示方式称为
编码(encoding)
先考虑如何表示自然数
生活中使用十进制(decimal)计数法, 真值可通过加权求和展开式得到:
\[734 = 10^2\times7+10^1\times3+10^0\times4\]
对于\(n\)位\(b\)进制数\(a_{n-1}a_{n-2}\dots a_1a_0\), 其真值为:
\[\sum_{i=0}^{n-1}a_ib^i=a_{n-1}b^{n-1}+a_{n-2}b^{n-2}+\dots+a_1b^1+a_0\]
其中\(b\)称为基(base), \(b^i\)称为每一位的权(weight)
二进制计数法
\[\sum_{i=0}^{n-1}a_ib^i=a_{n-1}b^{n-1}+a_{n-2}b^{n-2}+\dots+a_1b^1+a_0\]
令\(b=2\), 并让\(a_i\)只在0和1中取值,
得到二进制(binary)计数法:
\[\sum_{i=0}^{n-1}a_i2^i=a_{n-1}2^{n-1}+a_{n-2}2^{n-2}+\dots+a_12^1+a_0\]
例如, 二进制数0b101110的真值是
\[2^5\times1+2^4\times0+2^3\times1+2^2\times1+2^1\times1+2^0\times0=46\]
将十进制转换为二进制
需要求出加权求和展开式中各个二进制位\(a_{n-1}a_{n-2}\dots a_1a_0\)
可以将加权求和展开式改写如下: \[\begin{array}{ll} & \displaystyle \sum_{i=0}^{n-1}a_i2^i \\ &=a_{n-1}2^{n-1}+a_{n-2}2^{n-2}+\dots+a_12^1+a_0 \\ &=(a_{n-1}2^{n-2}+a_{n-2}2^{n-3}+\dots+a_1)\times2+a_0 \\ &=((a_{n-1}2^{n-3}+a_{n-2}2^{n-4}+\dots+a_2)\times2+a_1)\times2+a_0 \\ &=\dots \\ &=(\dots((a_{n-1}\times2+a_{n-2})\times2+a_{n-3})\dots)\times2+a_0 \\ \end{array}\]
发现: 如果将十进制数不断除以2, 这个过程中得到的余数就分别对应\(a_0,a_1,\dots,a_{n-1}\)
将十进制转换为二进制: 短除法
\[\sum_{i=0}^{n-1}a_i2^i = (\dots((a_{n-1}\times2+a_{n-2})\times2+a_{n-3})\dots)\times2+a_0\]
对于十进制数46:
2 | 46 -> 0 ^ 低位
+---- |
2 | 23 -> 1 |
+---- |
2 | 11 -> 1 |
+---- |
2 | 5 -> 1 |
+---- |
2 | 2 -> 0 |
+---- |
2 | 1 -> 1 | 高位
+----
0 (商为0, 结束)将所得余数从高位到低位组合, 得到0b101110,
即为46的二进制表示
\[2^5\times1+2^4\times0+2^3\times1+2^2\times1+2^1\times1+2^0\times0=46\]
十六进制计数法
二进制能被数字电路(门电路)直接处理, 但很难阅读和记忆
- 在二进制数和十进制数之间互相转换, 需要经过一定的数学计算过程
0b1011111011101111
计算机领域还通常采用十六进制(hexadecimal)计数法
- 每一位数字有16种可能, 除了
0~9以外, 还有a,b,c,d,e,f(大写亦可), 数值上分别表示10,11,12,13,14,15 - 在十进制和十六进制之间进行转换, 可以通过加权求和展开式和短除法来进行
例如, 十六进制数0xbeef的加权求和展开式如下: \[16^3\times11+16^2\times14+16^1\times14+16^0\times15=48879\]
十六进制和二进制之间的快速转换
数字电路无法直接处理十六进制数
但由于\(16=2^4\), 故能在1位十六进制数和4位二进制数之间快速转换
例如, 对于二进制数0b1011111011101111,
从右到左每4位分成一组(高位不足4位时补0),
直接写出每组对应的十六进制数字:
因此, 该二进制数对应的十六进制数即为0xbeef
和二进制表示的0b1011111011101111相比,
十六进制表示的0xbeef更加简洁紧凑
通过门电路搭建基本组合逻辑电路
译码器: n选1译码器
译码器 = 一种将\(k\)位输入转换成最多\(2^k\)种不同输出的电路
一类常见的译码器是n选1译码器
- 将\(n\)位输入看成真值\(x\), 使\(2^n\)位输出中仅第\(x\)位为
1(独热码(One-hot)) - 常用于寻址: 输入地址, 生成相应选择信号(地址\(\approx\)Excel表中的行号)
例: 2-4译码器
| \(A_1\) | \(A_0\) | \(|\) | \(Y_3\) | \(Y_2\) | \(Y_1\) | \(Y_0\) |
|---|---|---|---|---|---|---|
| 0 | 0 | \(|\) | 0 | 0 | 0 | 1 |
| 0 | 1 | \(|\) | 0 | 0 | 1 | 0 |
| 1 | 0 | \(|\) | 0 | 1 | 0 | 0 |
| 1 | 1 | \(|\) | 1 | 0 | 0 | 0 |
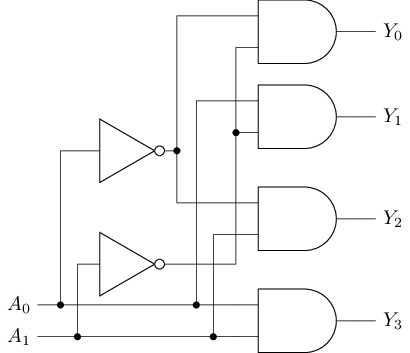
译码器: 转码器
按照指定的规则将一种编码的输入转换成另一种编码的输出
- 和n选1译码器不同, 转码器不要求输出中最多包含1个
1
常见应用: 七段数码管译码器(7-segment decoder)
- 七段数码管 = 由7段发光二极管按
8字型排列成的输出元件- 由8个控制信号控制(7+1个小数点)
- 只要某控制信号有效, 就会点亮相应的发光二极管
- 七段数码管译码器: 将一组4位的输入信号解析为二进制数, 输出一组控制信号, 用于控制七段数码管显示和输入对应的数字
a
---
f| g |b input output | |
--- abcdefgh ---
e| |c 0100 01100110 |
--- .h
d可列出真值表, 推导出每个控制信号的逻辑表达式, 得到电路层实现
编码器
功能和n选1译码器相反, 用于将独热码转换成相应的二进制数值
- 若输入为\(2^n\)位独热码, 且第\(x\)位为1, 则输出\(n\)位真值为\(x\)的二进制数
- 若输入不为独热码, 则输出是未定义(undefined)的
- 用途: 根据独热码生成地址; 找出独热码中
1的位置
例: 4-2编码器
| \(A_3\) | \(A_2\) | \(A_1\) | \(A_0\) | \(|\) | \(Y_1\) | \(Y_0\) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | \(|\) | 0 | 0 |
| 0 | 0 | 1 | 0 | \(|\) | 0 | 1 |
| 0 | 1 | 0 | 0 | \(|\) | 1 | 0 |
| 1 | 0 | 0 | 0 | \(|\) | 1 | 1 |
| 其 | 他 | 情 | 况 | \(|\) | 0 | 0 |

理解未定义的输出
一些运算或模块需要满足一定的前提条件, 才能得到有意义的输出
- 数学上的除法运算, 需要满足
除数不为0的前提条件- 除数为
0时, 除法运算的结果是未定义的
- 除数为
输入为独热码是编码器正确工作的前提条件- 输入不为独热码时, 编码器的输出是未定义的
背后的约定:
- 如果编码器的使用者希望编码器能输出正确的结果,
就需要保证
输入为独热码 - 如果不满足前提条件, 算是使用者违反约定
- 此时编码器的输出是无意义的
- 如果后续电路对这些无意义的输出进行处理, 结果由使用者承担
利用未定义情况简化编码器的设计
具体到数字电路层次, 编码器的输出信号要么为0,
要么为1
- 但在输出结果未定义的情况下, 无论输出信号取什么值, 都不具备实际含义
- 编码器的设计者可以为这些未定义情况下的输出信号取任意值
- 根据约定, 编码器的使用者不应该让后续电路处理那些未定义的输出信号
优先编码器
可支持独热码以外的输入, 但只编码优先级最高的位
- 若输入不全为
0, 则输出最高位的1的位置 - 若输入全为
0, 则输出是未定义的
例: 4-2优先编码器
| \(A_3\) | \(A_2\) | \(A_1\) | \(A_0\) | \(|\) | \(Y_1\) | \(Y_0\) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | \(|\) | 0 | 0 |
| 0 | 0 | 1 | X | \(|\) | 0 | 1 |
| 0 | 1 | X | X | \(|\) | 1 | 0 |
| 1 | X | X | X | \(|\) | 1 | 1 |
| 0 | 0 | 0 | 0 | \(|\) | X | X |
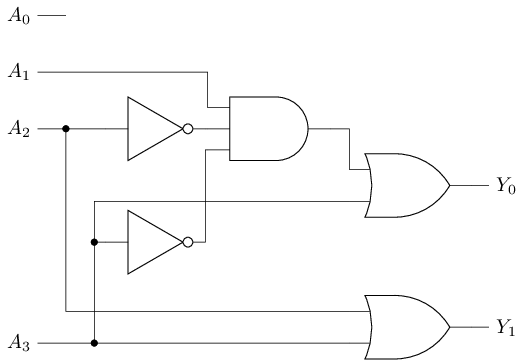
多路选择器
根据选择端选择一路输入
- 将选择端看作地址,则类似一次寻址操作
- 用来对数据来源和处理结果进行选择
例: 2选1多路选择器
| \(S\) | \(|\) | \(Y\) |
|---|---|---|
| 0 | \(|\) | \(D_0\) |
| 1 | \(|\) | \(D_1\) |
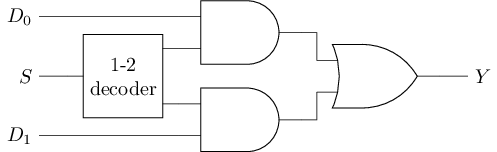

译码器生成的独热码作为数据的选择信号, 只有一路数据可以通过与门
#T(2-1 mux) = #T(1-2 dec) + 2#T(and) + #(or) = #T(not) + 2 * 8 + 8 = 26
#T(2-1 mux32) = #T(1-2 dec) + 32(2#T(and) + #(or)) = 2 + 32 * (2 * 8 + 8) = 770对于数据位宽为\(M\)位的\(N\)选1多路选择器, \(\log_{2}{N}\)-\(N\)译码器的输出只有1位为1,
且可被\(M\)个\(N\)选1多路选择器复用
用传输门实现多路选择器
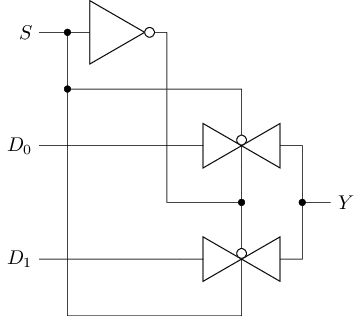
\(S\)只会导通其中一个传输门, 另一个截止, 从而实现数据选择功能
比较器
检查两个输入的每一位是否完全一致
例: 4位比较器
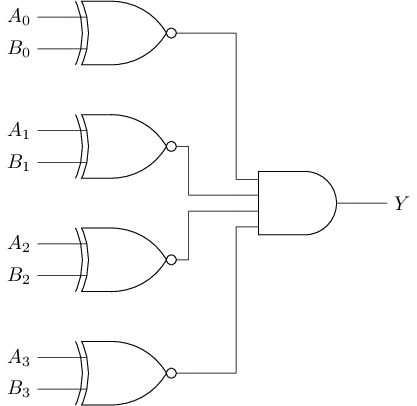
#T(cmp4) = 4#T(xnor) + #T(and4) = 4 * 6 + (4 - 1) * 8 = 48
#T(cmp32) = 32#T(xnor) + #T(and32) = 32 * 6 + (32 - 1) * 8 = 4401位加法器
半加器(Half Adder, HA), 输入无进位的加法器
#T(HA) = #T(xor) + #T(and) = 6 + 8 = 14全加器(Full Adder, FA), 输入有进位的加法器
| \(A\) | \(B\) | \(|\) | \(S\) | \(C\) |
|---|---|---|---|---|
| 0 | 0 | \(|\) | 0 | 0 |
| 0 | 1 | \(|\) | 1 | 0 |
| 1 | 0 | \(|\) | 1 | 0 |
| 1 | 1 | \(|\) | 0 | 1 |
可以用两个半加器组成一个全加器
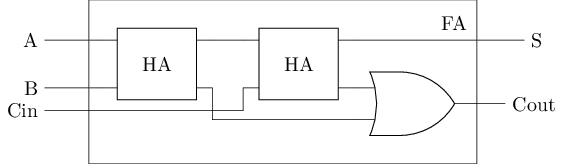
#T(FA) = 2#T(HA) + #T(or) = 2 * 14 + 8 = 36多位加法器
将低位FA的进位输出作为高位FA的进位输入
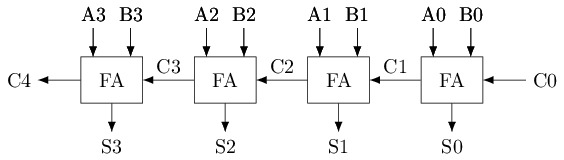
行波进位加法器(Ripple-Carry Adder, RCA)
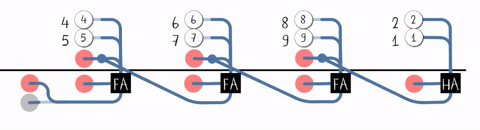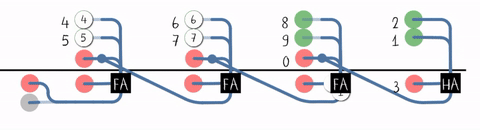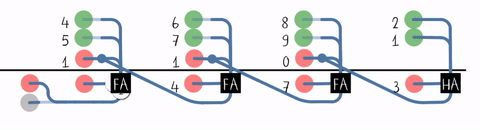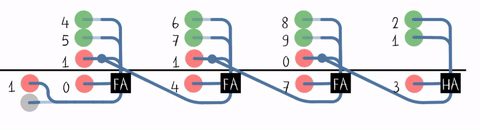
#T(RCA4) = #(HA) + 3#T(FA) = 14 + 3 * 36 = 122
#T(RCA32) = #(HA) + 31#T(FA) = 14 + 31 * 36 = 1130总结
MOS -> CMOS -> 门电路 -> 组合逻辑电路
- 用nMOS和pMOS实现开关
- 用MOS管的开关特性实现CMOS中的
0和1
- 通过晶体管搭建门电路进行
0和1的简单运算- not, nand, and, nor, or, xor, xnor
- 用多位
0和1表示自然数- 二进制计数法, 十六进制计数法
- 通过门电路搭建组合逻辑电路处理信息
- 译码器, 编码器, 多路选择器, 比较器, 加法器