
通知
下次课时间提前到2023/01/21 15:00~17:00
引言
我们之前都是用+,
*等直接实现加法和乘法的功能
本次课内容: 了解这些功能单元如何设计
- 加法器
- 乘法器
- 除法器
加法器
数字电路课上的1位加法器
可以用两个半加器组成一个全加器
多位加法器
A3 B3 A2 B2 A1 B1 A0 B0
| | | | | | | |
V V V V V V V V
+----+ C3 +----+ C2 +----+ C1 +----+
C4<--| FA |<---| FA |<---| FA |<---| FA |<--C0
+----+ +----+ +----+ +----+
| | | |
V V V V
S3 S2 S1 S0行波进位加法器(Ripple-Carry Adder, RCA)
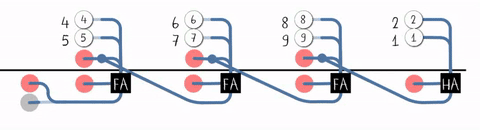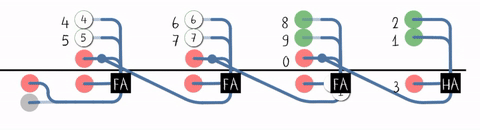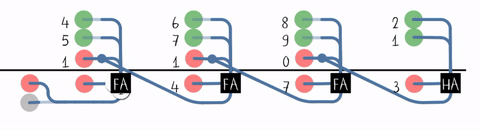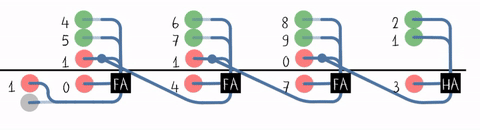
近距离观察进位
新的解读
- 若G为1, 则Cout必定为1
- G = A & B可用于产生(Generate)当前位的进位
- 若G为0且P为1, 则Cout与Cin相同
- P = A ^ B可用于将低位进位传播(Propagate)到当前位的进位输出
对于4位加法器
更快的进位计算方法
C1 = G0 | (C0 & P0)
C2 = G1 | (C1 & P1) = G1 | ((G0 | (C0 & P0)) & P1) = G1 | (G0 & P1) | (C0 & P0 & P1)
C3 = G2 | (C2 & P2) = G2 | (G1 & P2) | (G0 & P1 & P2) | (C0 & P0 & P1 & P2)
C4 = G3 | (G2 & P3) | (G1 & P2 & P3) | (G0 & P1 & P2 & P3) | (C0 & P0 & P1 & P2 & P3)G和P只依赖加法器的输入, 不依赖每一位的进位!
设\(D(signal)\)为计算signal的门延迟级数, 设\(d\)为1级门延迟
- \(D(G) = D(P) = d\)
- \(D(C_i) = 3d, i > 1\)(多1级与门和1级或门)
- \(D(S_i) = 4d, i > 1\)(多1级异或门)
这就是先行进位加法器(Carry-Lookahead Adder, CLA)
- \(D(C_i) < D(S_i)\)
CLA vs. RCA
C4 = (A3 & B3) | (C3 & (A3 ^ B3))
= (A3 & B3) | (((A2 & B2) | (C2 & (A2 ^ B2))) & (A3 ^ B3)) = ...
= (A3 & B3) | (((A2 & B2) | (((A1 & B1) | (((A0 & B0) | (C0 & (A0 ^ B0)))
& (A1 & B1))) & (A2 ^ B2))) & (A3 ^ B3))4位RCA中4个FA级联, 每经过一个FA计算C需额外\(2d\)
- \(D(C_1) = 3d\)
- \(D(C_i) = D(C_1) + 2d * (i - 1) = (2i +
1)d, i > 1\)
- \(D(C_4) = 9d\)
- \(D(S_i) = D(C_i) + d = 2(i+1)d, i >
1\)
- \(D(S_3) = 8d\)
从逻辑表达式看CLA更优的本质: 通过表达式变换对电路进行平衡处理
// 2位RCA的电路
+-----+
C0-----------------| |
+-----+ | and |--+
A0---+--| | +--| | |
| | xor |-+ +-----+ | +----+
B0-+----| | +--| |
| | +-----+ | or |--+
| | +--| | |
| | +-----+ | +----+ |
| +--| | | | +-----+
| | and |-------------+ +--| |
+----| | | and |--+
+-----+ +--| | |
| +-----+ |
+-----+ | |
A1---+--| | | | +----+
| | xor |------------------------+ +--| |
B1-+----| | | or |----C2
| | +-----+ +--| |
| | | +----+
| | +-----+ |
| +--| | |
| | and |------------------------------------+
+----| |
+-----+分组CLA
C4 = G3 | (G2 & P3) | (G1 & P2 & P3) | (G0 & P1 & P2 & P3) | (C0 & P0 & P1 & P2 & P3)
C64 = G63 | (G62 & P63) | (G61 & P62 & P63) | (G60 & P61 & P62 & P63) | ...原则上来说, 位宽更大的CLA也可以通过上述方式搭建
- \(D(C_i)=3d, i > 1\)同样成立
- 但与门和或门输入太多, 延迟也会增加
4位CLA
A3B3 A2B2 A1B1 A0B0
|| || || ||
+---------------------------------------------+
S0<--|------||--------||--------||------+ || |
S1<--|------||--------||------+ || | || |
S2<--|------||------+ || | || | || |
S3<--|-+ VV | VV | VV | VV |
| | +----+ +----+ +----+ +----+ |
| +-| FA |<-+ | FA |<-+ | FA |<-+ | FA |<--+--|--C0
| +----+ | +----+ | +----+ | +----+ | |
| || | || | || | || | |
| VV | VV | VV | VV | |
| +------------------------------------+ | |
| | P3G3 C3 P2G2 C2 P1G1 C1 P0G0| | |
C4<--|--|C4 Carry Lookahead Unit(CLU) |<-+ |
| | PG GG | |
| +------------------------------------+ |
| 4-bit Carry-Lookahead Adder | | |
+---------------------------------------------+
| |
V V16位CLA
A/B12~15 A/B8~11 A/B4~7 A/B0~3
|| || || ||
+---------------------------------------------+
S0~3 <--|------||--------||--------||------+ || |
S4~7 <--|------||--------||------+ || | || |
S8~11 <--|------||------+ || | || | || |
S12~15<--|-+ VV | VV | VV | VV |
| | +----+ +----+ +----+ +----+ |
| +-|4CLA|<-+ |4CLA|<-+ |4CLA|<-+ |4CLA|<--+--|--C0
| +----+ | +----+ | +----+ | +----+ | |
| || | || | || | || | |
| VV | VV | VV | VV | |
| +------------------------------------+ | |
| | P3G3 C12 P2G2 C8 P1G1 C4 P0G0| | |
C16 <--|--|C16 Carry Lookahead Unit(CLU) |<-+ |
| | PG GG | |
| +------------------------------------+ |
| 16-bit Carry-Lookahead Adder | | |
+---------------------------------------------+
| |
V V同理, 64位CLA可以通过4个16位CLA和1个CLU组合搭建
16位CLA的延迟
- 每个FA: \(D(P) = D(G) = d\)
- 每个4位CLA: \(D(PG) = 2d, D(GG) = 3d\)
- 组间进位\(D(C_{\{4, 8, 12, 16\}}) = 5d\)
- 组内进位
- \(D(C_{\{1,2,3\}}) = 3d\)
- \(D(C_{\{5,6,7,9,10,11,13,14,15\}}) = 7d\)
- 计算S
- \(D(S_0) = d\)
- \(D(S_{\{1,2,3\}}) = 4d\)
- \(D(S_{\{4, 8, 12\}}) = 6d\)
- \(D(S_{\{5,6,7,9,10,11,13,14,15\}}) = 8d\)
A/B12~15 A/B8~11 A/B4~7 A/B0~3
|| || || ||
+---------------------------------------------+
S0~3 <--|------||--------||--------||------+ || |
S4~7 <--|------||--------||------+ || | || |
S8~11 <--|------||------+ || | || | || |
S12~15<--|-+ VV | VV | VV | VV |
| | +----+ +----+ +----+ +----+ |
| +-|4CLA|<-+ |4CLA|<-+ |4CLA|<-+ |4CLA|<--+--|--C0
| +----+ | +----+ | +----+ | +----+ | |
| || | || | || | || | |
| VV | VV | VV | VV | |
| +------------------------------------+ | |
| | P3G3 C12 P2G2 C8 P1G1 C4 P0G0| | |
C16 <--|--|C16 Carry Lookahead Unit(CLU) |<-+ |
| | PG GG | |
| +------------------------------------+ |
| 16-bit Carry-Lookahead Adder | | |
+---------------------------------------------+
| |
V V16位RCA
- \(D(C_16) = (2 * 16 + 1)d = 33d\)
- \(D(S_15) = 2 * (15 + 1)d = 32d\)
减法器
将1输入到加法器的\(C_0\), 可通过加法器实现减法器
若无需同时完成加法和减法操作, 可让两者共享同一个加法器
RTL中直接用+/-, 综合器通常能直接生成CLA
- 可以查看Vivado/yosys生成的网表文件
3个数相加
一种方法: 采用两个CLA, 先计算T = A + B, 再计算S = T + C
+----+ +----+
A-->| |--------------->| |-->S
B-->| FA | C-->| FA |
Cin-->| |-->Cout Cin-->| |-->Cout
+----+ +----+- 假设A, B, C均为16位, 则\(D(S_{15}) = 2 * 8d = 16d\)
可以再快一些吗?
回顾: 在多位加法器中, FA的Cin需要一段延迟才能到达
一个想法: 能否把第一个CLA中的进位处理合并到第二个CLA中?
将和与进位分离
先计算3个数 “不进位的和”与 “进位”, 再将其相加得到最终的和
- 一个例子
保留进位加法器(Carry-Save Adder, CSA)
- 第一个加法器将3个数按位相加, 得到 “不进位的和”与 “进位”
- 将加法的进位保留下来, 称为CSA
- “不进位的和”与保留的进位输入到第二个加法器, 计算最终的和
- 进位要左移一位
+----+ | | +----+
A4-->| |------+ | +-->| |-->S4
B4-->| FA | | +----->| FA |
C4-->| |---+ +-------->| |--+
+----+ | +----+ |
+-----+ +-----------+
+----+ | | +----+
A5-->| |------+ | +-->| |-->S5
B5-->| FA | | +----->| FA |
C5-->| |---+ +-------->| |--+
+----+ | +----+ |
+-----+ +-----------+
+----+ | | +----+
A6-->| |------+ | +-->| |-->S6
B6-->| FA | | +----->| FA |
C6-->| |---+ +-------->| |--+
+----+ | +----+ |为方便理解, 第二个加法器使用RCA
CSA延迟与1-bit FA相同
- 计算 “不进位的和”延迟为\(d\), 计算 “进位”延迟为\(3d\)
- 若第二个加法器使用CLA, 则采用CSA将3个数16位数相加的延迟为\(3d+8d=11d\)
乘法器
补码乘法
假设\(A\)和\(B\)均为8位补码表示, 且\(B=b_7b_6b_5b_4b_3b_2b_1b_0\)
\(A\times B = A\times (-b_7 * 2^7 + b_6 * 2^6 + b_5 * 2^5 + \dots + b_0 * 2^0)\)
\(= A\times (-b_7 * 2^7 + (b_6 * 2^7 - b_6 * 2^6) + (b_5 * 2^6 - b_5 * 2^5) + \dots + (b_0 * 2^1 - b_0 * 2^0))\)
\(= A\times ((b_6-b_7) * 2^7 + (b_5-b_6) * 2^6 + \dots + (b_0 - b_1) * 2^1 + (0 - b_0) * 2^0)\)
\(= (b_6-b_7)A * 2^7 + (b_5-b_6)A * 2^6 + \dots + (b_0 - b_1)A * 2^1 + (0 - b_0)A * 2^0\)
\(= (b_6-b_7)A * 2^8 * 2^{-1} + (b_5-b_6)A * 2^8 * 2^{-2} + \dots + (b_0 - b_1)A * 2^8 * 2^{-7} + (0 - b_0)A * 2^8 * 2^{-8}\)
令\(b_{-1}=0\), \(P(0)=0\), \(P(i+1)=2^{-1}(P(i)+(b_{i-1}-b_i)A * 2^8)\)
则\(A\times B = P(8)\)
Booth’s Algorithm
根据递推公式\(P(i+1)=2^{-1}(P(i)+(b_{i-1}-b_i)A * 2^8)\)设计乘法器电路
一种实现方式 - 多周期循环移位加法
- 维护部分积\(P\)和加数\(S\), 开始计算时\(P=0\), \(S=A * 2^8=\{A, 8'b0\}\)
- 在第\(i\)次循环时, 根据乘数\(\{b_i,b_{i-1}\}\)的取值, 选择相应的操作更新\(P\)
- 将\(P\)算术右移1位
| \(\{b_i,b_{i-1}\}\) | \(P\)的操作 |
|---|---|
| 00 | \(+0\) |
| 01 | \(+S\) |
| 10 | \(-S\) |
| 11 | \(+0\) |
- 若\(i=8\), 则结束, 此时\(P\)为最后乘积; 否则\(i=i+1\), 进行下一次循环
RTL实现 = 状态机 + 总线
- 用状态机控制循环次数
- 用握手信号控制乘法器与上下游模块的通信
减少循环次数
如果\(A\)和\(B\)有64位, 则上述乘法器需要循环64周期才能计算一次乘法
为了减少循环次数, 可以在一次循环中扫描乘数中更多的位
- 需要推导出\(P(i+2)\)关于\(P(i)\)的递推公式
\(P(i+1)=2^{-1}(P(i)+(b_{i-1}-b_i)A * 2^8)\)
\(P(i+2)=2^{-1}(P(i+1)+(b_{i}-b_{i+1})A * 2^8)\)
\(=2^{-1}(2^{-1}(P(i)+(b_{i-1}-b_i)A * 2^8)+(b_{i}-b_{i+1})A * 2^8)\)
\(=2^{-2}(P(i)+(b_{i-1}-b_i)A * 2^8+(2b_{i}-2b_{i+1})A * 2^8)\)
\(=2^{-2}(P(i)+(b_{i-1}+b_i-2b_{i+1})A * 2^8)\)
Radix-4 Booth’s Algorithm
根据递推公式\(P(i+2)=2^{-2}(P(i)+(b_{i-1}+b_i-2b_{i+1})A * 2^8)\)设计乘法器电路
- 维护部分积\(P\)和加数\(S\), 开始计算时\(P=0\), \(S=A * 2^8=\{A, 8'b0\}\)
- 在第\(i\)次循环时, 根据乘数\(\{b_{i+1},b_i,b_{i-1}\}\)的取值, 选择相应的操作更新\(P\)
- 将\(P\)算术右移2位
- 若\(i=8\), 则结束, 此时\(P\)为最后乘积; 否则\(i=i+2\), 进行下一次循环
对于64位乘法, 基4-Booth算法只需循环32次
| \(\{b_{i+1},b_i,b_{i-1}\}\) | \(P\)的操作 |
|---|---|
| 000 | \(+0\) |
| 001 | \(+S\) |
| 010 | \(+S\) |
| 011 | \(+2S\) |
| 100 | \(-2S\) |
| 101 | \(-S\) |
| 110 | \(-S\) |
| 111 | \(+0\) |
还能更快吗?
快速乘法器 - 让我们在一个周期内算出结果
把Booth算法中每次循环选出的操作一次性全部选好并相加
- 回到了小学笔算乘法, 只不过我们需要用组合电路实现
// 以16位乘法为例, 采用基4-Booth算法
10987654321098765432109876543210
sssssssssssssss***************** s = the sign bit of the partial product
sssssssssssss***************** ' ' = 0
sssssssssss*****************
sssssssss*****************
sssssss*****************
sssss*****************
sss*****************
+ s*****************
----------------------------------
******************************** <- A * B
直接在Verilog中写*, 就会综合出这种乘法器
- 不过我们先来看看它如何设计
一些优化
sssssssssssssss***************** n***************** n*****************
sssssssssssss***************** n***************** n*****************
sssssssssss***************** n***************** n*****************
(1) sssssssss***************** (2) n***************** (3) n*****************
sssssss***************** n***************** n*****************
sssss***************** n***************** n*****************
sss***************** n***************** n*****************
s***************** n***************** n = ~s n*****************
- 1 1 1 1 1 1 1 1 + 01010101010101011111111111111111
+ 1
n***************** nss***************** nss*****************
n***************** 1n***************** 1n*****************xy
n***************** 1n***************** 1n*****************xy
(4) n***************** (5) 1n***************** (6) 1n*****************xy
n***************** 1n***************** 1n*****************xy
n***************** 1n***************** 1n*****************xy
n***************** 1n***************** 1n*****************xy
n***************** n***************** n*****************xy
+ 010101010101011 (6)中的xy为降低基4-Booth算法中的\(-S\)和\(-2S\)计算延迟而添加的修正项
- \(-S=\sim S+1\), \(-2S=2(\sim S+1)=2 * (\sim S)+2\),
加法器引入进位延迟
- 故通过若干变换将其计算移动到部分积中
- 考虑上一行部分积, 若为\(-S\), 则当前行的x=0, y=1; 若为\(-2S\), 则当前行的x=1, y=0; 其他情况, 则当前行的x=0, y=0
华莱士树(Wallace Tree)压缩
10987654321098765432109876543210 10987654321098765432109876543210 10987654321098765432109876543210
nss***************** ******************** ********************************
1n*****************xy ********************* *******************************
1n*****************xy ********************* ***************************
(6) 1n*****************xy (7) ********************* (8) ***********************
1n*****************xy ********************* *******************
1n*****************xy ********************* ^ *************** ^
1n*****************xy ********************* | *********** |
n*****************xy ******************** ********我们希望高效地对多个数求和
华莱士树压缩的目标: 通过CSA对上述部分积的树排列进行压缩, 并正确维护进位的位置
- 对所有列压缩一次后形成一层, 可能需要多层压缩
- 直到树的高度为2, 表示已压缩为2个数, 可用CLA直接求和
华莱士树压缩算法

while (tree.maxheight > 2) { // need a new layer to compress
for (col = 0; col < N*2; col ++) {
while (col.height > 0) {
switch (col.height) {
case 0: break;
case 1: (s, c) = (col, NULL); col = col.drop(1); break;
case 2: (s, c) = HA(col); col = col.drop(2); break;
case 3: (s, c) = FA(col); col = col.drop(3); break;
default: (s, c) = FA(col.take(3));
col = col.drop(3); break;
}
col.add_next_turn(s);
(col + 1).add_next_turn(c);
}
}
}
result = tree.row(0) + tree.row(1);从压缩率来看, FA(3->2)比HA(2->2)更优
- HA的作用: 虽然不能直接压缩高度, 但可以将1个bit移动到左边列, 增加其通过FA压缩的机会
进一步降低延迟: 插入寄存器给压缩过程分阶段, 用状态机/流水线控制
更多种类的压缩器
有研究提到可以使用更多的压缩器(4-2, 6-2, 9-2)来进行树压缩
4-2压缩器由两个FA组成, 有3种输出
- 留在本列的和s, 参与下一层本列的压缩
- 输出到左边列且与当前压缩器的cin输入无关的进位cout1, 参与本层左边列的压缩
- 输出到左边列且与当前压缩器的cin输入相关的进位cout2,
参与下一层左边列的压缩
- 避免进位延迟横向传播较远
colunm i+1 colunm i
in1 in2 in1 in2
| | | |
+----------+ +----------+
| | | | | | | |
| V V | | V V |
| +----+ | | +----+ |
cout1<--|-| FA |<--|-- in3 +---|-| FA |<--|-- in3
| +----+ | | | +----+ |
| | +---|-- in4 | | | +---|-- in4
| | | | | | | | |
| V V | +-+ | V V |
| +----+ | cin | | +----+ |
cout2<--|--| FA |<-|-----+ +---|--| FA |<-|-- cin
| +----+ | | | +----+ |
| | | | | | |
+----------+ | +----------+
| | |
V s cout2 V V s
+-------------------------------------+
| Next Layer |
+-------------------------------------+
复杂压缩器可压缩更多高度, 减少层数(外层while循环次数), 但延迟较高
- 使用哪些压缩器以何种方案进行压缩, 是一个设计空间探索问题
Chisel重磅福利
香山团队成员ljw, Implementation of a Highly Configurable Wallace Tree Multiplier with Chisel @ Chisel Community Conference 2021, RISC-V中国峰会同地活动
def addOneColumn(col: Seq[Bool], cin: Seq[Bool]):
(Seq[Bool], Seq[Bool], Seq[Bool]) = {
var sum = Seq[Bool]()
var cout1 = Seq[Bool]()
var cout2 = Seq[Bool]()
col.size match {
case 1 => // do nothing
sum = col ++ cin
case 2 =>
val c22 = Module(new C22)
c22.io.in := col
sum = c22.io.out(0).asBool() +: cin
cout2 = Seq(c22.io.out(1).asBool())
case 3 =>
val c32 = Module(new C32)
c32.io.in := col
sum = c32.io.out(0).asBool() +: cin
cout2 = Seq(c32.io.out(1).asBool())
case 4 =>
val c53 = Module(new C53)
for((x, y) <- c53.io.in.take(4) zip col){
x := y
}
c53.io.in.last := (if(cin.nonEmpty) cin.head else 0.U)
sum = Seq(c53.io.out(0).asBool()) ++ (if(cin.nonEmpty) cin.drop(1) else Nil)
cout1 = Seq(c53.io.out(1).asBool())
cout2 = Seq(c53.io.out(2).asBool())
case n =>
val cin_1 = if(cin.nonEmpty) Seq(cin.head) else Nil
val cin_2 = if(cin.nonEmpty) cin.drop(1) else Nil
val (s_1, c_1_1, c_1_2) = addOneColumn(col take 4, cin_1)
val (s_2, c_2_1, c_2_2) = addOneColumn(col drop 4, cin_2)
sum = s_1 ++ s_2
cout1 = c_1_1 ++ c_2_1
cout2 = c_1_2 ++ c_2_2
}
(sum, cout1, cout2)
}def addAll(cols: Array[Seq[Bool]], depth: Int):
(UInt, UInt) = {
if(max(cols.map(_.size)) <= 2){
val sum = Cat(cols.map(_(0)).reverse)
var k = 0
while(cols(k).size == 1) k = k+1
val carry = Cat(cols.drop(k).map(_(1)).reverse)
(sum, Cat(carry, 0.U(k.W)))
} else {
val columns_next = Array.fill(2*len)(Seq[Bool]())
var cout1, cout2 = Seq[Bool]()
for( i <- cols.indices){
val (s, c1, c2) = addOneColumn(cols(i), cout1)
columns_next(i) = s ++ cout2
cout1 = c1
cout2 = c2
}
val needReg = depth == 4
val toNextLayer = if(needReg)
columns_next.map(_.map(
x => RegEnable(x, io.regEnables(1))))
else
columns_next
addAll(toNextLayer, depth+1)
}
}
val columns_reg = columns.map(col => col.map(
b => RegEnable(b, io.regEnables(0))))
val (sum, carry) = addAll(columns_reg, 0)
io.result := sum + carry通过递归实现华莱士树
Chisel福利的本质 - 不当工具人
华莱士树压缩算法描述了如何实例化各种CSA并连线
- 执行这个算法, 就能得到RTL层次的华莱士树
关键是谁来执行这个算法
- 传统RTL设计流程 - 程序员来执行, 需要手动编排CSA和连线
- 如果算法的输入有变化, 程序员需要重新执行
- 乘法器位宽, 优化Booth算法, 优化树外型, 使用新CSA…
- 如果算法的输入有变化, 程序员需要重新执行
- Chisel流程 - Chisel Builder(一个Scala程序)来执行
- 用Chisel写的不是华莱士树, 而是华莱士树生成器(generator)
- 如果算法的输入有变化, 只需对这个描述算法的Scala程序稍作修改, 重新运行即可
传统流程也可以使用perl/tcl等脚本编写这个算法来生成RTL代码
- 但这些语言和Verilog的结合远不如Scala和Chisel的结合紧密
乘法器作为专用加速器
两种在无乘法器的处理器上计算乘法的方式
- 非法指令异常 + 软件模拟
- 识别到乘法指令后, 通过软件循环移位加法来计算乘法
- 本质上是用RV64I指令来模拟乘法的计算过程
- 编译 + 链接
- gcc识别到乘法操作后, 生成一条跳转到库函数的指令
- 然后链接到gcc的算术库, 该算术库仍通过RV64I指令模拟乘法计算
#include <stdio.h>
int f(int a, int b) { return a * b; }
int main() { printf("%d\n", f(2, 3)); return 0; }
如果把乘法器看成专用加速器, 其加速效果能到1~2个数量级
Chisel重磅福利第二弹 - 形式化验证
形式化验证
华莱士树这么复杂, 连错一根线, 乘法结果就错了
- 测试有点困难 - 全覆盖时间开销太大, 自己写测试又怕漏了哪个case
- 调试也很麻烦 - 你不太容易知道每个CSA在正确的时候应该输出什么
针对第一个问题, 形式化验证方法可以帮助我们
求解器(Solver)是形式化验证方法的核心
- 将约束(验证条件)用求解器识别的语言表达出来
- 尝试让求解器求解 “至少一个约束不成立”的输入是否存在 - 类似解方程
- 若存在, 则找到一个可以让设计出错的反例
- 若不存在, 则说明所有输入都满足给定的约束
- 例如,
若某设计中有
assert(cond1)和assert(cond2), 则尝试求解是否存在输入使得!cond1 || !cond2成立
Z3 - SMT solver
Z3是一个可满足性模理论(Satisfiablity Modulo Theories)求解器, 来自Microsoft Research
#!/usr/bin/python
from z3 import *
x = Real('x')
y = Real('y')
z = Real('z')
s = Solver()
s.add(3*x + 2*y - z == 1)
s.add(2*x - 2*y - 4*z == -2)
s.add(-x + 0.5*y - z == 0)
print(s.check())
print(s.model())还能够求解数独
Chisel重磅福利第二弹
Chisel的测试框架chiseltest可以将FIRRTL代码翻译成Z3识别的语言,
让Z3证明给定assert()是否正确
- 若能找到反例, 则生成该反例的波形, 辅助调试
- 香!
可让乘法器RTL计算结果与*对比
但对于复杂的设计, 求解复杂度较高, 导致运行时间很长
- 一般用于单元测试
import chisel3._
import chisel3.util._
import chiseltest._
import chisel3.experimental.BundleLiterals._
import chiseltest.formal._
import chiseltest.formal.BoundedCheck
import utest._
class Sub extends Module {
val io = IO(new Bundle {
val a = Input(UInt(4.W))
val b = Input(UInt(4.W))
val c = Output(UInt(4.W))
})
//val cnt = Counter(true.B, 16)._1
//io.c := io.a + ~io.b + Mux(cnt === 3.U, 2.U, 1.U)
io.c := io.a + ~io.b + 1.U
val ref = io.a - io.b
chisel3.assert(io.c === ref)
}
object Sub extends TestSuite {
val tests: Tests = Tests {
test("mytest") {
new Formal with HasTestName {
def getTestName: String = s"sub"
}.verify(new Sub, Seq(BoundedCheck(1)))
}
}
}除法器
除法器设计
原理与Booth算法相似, 可以采用多周期循环移位减法
- 有恢复余数法和不恢复余数法
- 还有高基SRT除法
- 通过查表选商
不过除法器难以实现流水化, 因此计算延迟通常比乘法器高
更多内容可STFW
总结
功能单元设计
- 加法器 - RCA, CLA, CSA
- 乘法器 - Booth算法, 基4-Booth算法, 华莱士树
- 用Chisel编写华莱士树生成器
- 用chiseltest进行形式化验证
- 除法器 - 恢复余数法, 不恢复余数法, 高基SRT除法
其实加法器和乘法器的应用已经很成熟了
- 在RTL中编写
+和*, 综合器通常能综合出低延迟的组合逻辑电路- 自己设计的加法器和乘法器, 通常比不过工具自带的结果
- 流水线乘法器也可以通过retiming技术让EDA工具在合适的位置自动插入触发器来实现
- 在 “一生一芯”学习过程中不必过分纠结一点点时序


